| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 심리학
- 강화
- 행동주의 치료
- 따뜻함주의
- 행동주의
- 외측 슬상핵
- ctm
- #산업및조직심리학
- individualism
- #크립키
- 연결주의
- 시각처리
- heartism
- 테스토스테론렉스
- persuation
- #정신역동
- 도덕발달단계론
- 일주율
- celtic knot
- #정신분석
- criminal psychology
- Psychology
- 켈트 매듭
- memory
- behavior modification
- sexdifference
- collectivism
- 빅토리아 시대
- 집단주의
- 개인주의
Archives
- Today
- Total
지식저장고
카이제곱분포로 모분산을 구간추정하는 방법 본문
먼저 이를 시행하기 전에 W에 대해 알아야 한다. W는 하나의 통계량으로 m을 μ대신 사용한 임의의 t점수를 합한 값이다. 예로, 무한개의 변환된 t점수를 합한 경우 W는 아래와 같다.
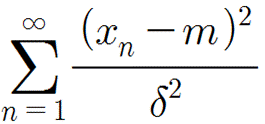
여기서 W는 s^2와 분자를 공유하고 있다는 유사점을 알 수 있을 것이다. 그래서 s^2에 n을 곱하고 모분산으로 나누면 W가 나온다.
1.먼저 표본에서 m을 구하고 표본 분산(s^2)을 구한다. 그리고 표본 분산에 n을 곱하고 모분산으로 나눠 W를 구한다.
2.W값은 자유도가 n-1인 상태로 카이제곱분포를 그린다. 카이제곱분포는 임의의 제곱한 z점수를 합한 것인데 n에 따라 모양이 다르지만 대체로 아래와 같다.
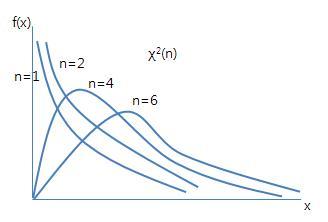
이 분포는 모두 제곱한 z점수로 이루어졌기 때문에 음수가 없어서, n이 적을 때에는 정규분포(더 가파른)를 반 접은 모양을 취한다. 그러나 n이 늘어날수록 카이제곱분포도 정규분포와 비슷해진다. 그리고 W도 자유도가 n-1인 상태로 카이제곱분포에 따른다. 그리고 우리는 합리적으로 우리가 가진 W가 다른 곳보다 중간의 95%구간에 있을 확률이 높다고 추론할 수 있다.
3.W가 카이제곱분포의 95%구간에 있다고 가정한다. 그러면 W는 k1≤W≤k2에 있게 된다. 이걸 이항하면 모분산의 구간을 추정할 수 있다.
'자료실' 카테고리의 다른 글
| t검정(t test) 절차 (0) | 2022.06.29 |
|---|---|
| 과학적 진리의 국소적 실재성에 대한 가설 (2) | 2022.06.29 |
| 신뢰구간을 이용한 t검정 (0) | 2022.06.28 |
| ANOVA(분산분석,F검정) 절차 (0) | 2022.05.24 |
| 아카이브 저장고(냉동) (0) | 2022.05.23 |
Comments



